파스칼의 삼각형

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요

파스칼의 삼각형은 각 행의 양 끝을 1로 시작하고, 각 숫자들은 바로 윗줄의 인접한 두 숫자의 합으로 채워지는 삼각형 모양의 숫자 배열이다. 이 삼각형은 동서양 여러 문화권에서 발견되었으며, 블레즈 파스칼의 이름을 따서 명명되었다. 파스칼의 삼각형은 이항 계수를 계산하는 데 사용되며, 이항 정리, 조합론, 확률 분포, 패턴 등 다양한 수학적 개념과 관련이 있다. 또한 컴퓨터 과학 분야에서도 프로그래밍 언어를 사용하여 구현될 수 있다.

더 읽어볼만한 페이지

블레즈 파스칼 - 파스칼 (단위)
파스칼(Pa)은 1 뉴턴의 힘이 1제곱미터의 면에 수직으로 가해질 때 작용하는 압력을 나타내는 SI 유도 단위이며, 블레즈 파스칼의 이름을 따서 명명되었고 다양한 분야에서 사용된다.
블레즈 파스칼 - 파스칼 정리
파스칼 정리는 원뿔 곡선 위의 여섯 점으로 이루어진 육각형의 대변 연장선들이 한 직선에서 만나는 기하학적 정리로, 블레즈 파스칼이 발견했으며 사영 기하학에서 중요한 역할을 하고 다양한 관련 정리와 원뿔 곡선 문제 해결에 활용된다.
인도의 발명품 - 이진법
이진법은 0과 1 두 개의 숫자를 사용하는 밑이 2인 위치 기수법으로, 컴퓨터 과학의 기초가 되었으며 현대 컴퓨터에서 데이터를 저장하고 처리하는 데 사용된다.
인도의 발명품 - 수차
수차는 물의 힘을 이용하여 회전력을 얻는 기계로, 고대부터 농지 관개나 맷돌 등에 사용되었으며, 충동 수차와 반동 수차로 분류되고, 최근에는 수력 터빈으로 발전하여 전력 생산에 활용된다.
계승과 이항식 주제 - 이항 정리
이항 정리는 이변수 다항식 (x + y)ⁿ을 전개하는 공식으로, 이항 계수를 사용하며, 조합론적 증명과 수학적 귀납법을 통해 증명할 수 있고, 다양한 분야에 응용되며, 이항 급수, 다항 정리 등 일반화된 형태가 존재한다.
계승과 이항식 주제 - 감마 분포
감마 분포는 형상 모수와 척도 모수로 정의되는 연속 확률 분포로, 확률 밀도 함수가 감마 함수로 표현되며, 베이즈 통계학에서 켤레 사전 분포로 활용되고, 형상 모수가 양의 정수일 때는 얼랑 분포를 나타낸다.

파스칼의 삼각형
개요
처음 6줄의 파스칼 삼각형
유형	수열
분야	수학
상세 정보
정의	이항 계수의 삼각형 배열
속성
대칭성	중앙 열을 기준으로 대칭
합	각 행의 합은 2의 거듭제곱 (이항 정리)
응용	조합론, 확률론, 대수학 등 다양한 분야에서 활용
역사
최초 연구	기원전 450년경 인도의 수학자 핑갈라가 처음 연구
이름 유래	17세기 프랑스 수학자 블레즈 파스칼의 이름을 따서 명명
다른 이름	중국: 양휘삼각형 이탈리아: 타르탈리아 삼각형
계산
이항 계수	n번째 행의 k번째 숫자는 이항 계수 와 같음
응용
이항 정리	이항 정리의 계수를 나타냄
조합론	조합의 수를 계산하는 데 사용
확률론	확률 분포를 계산하는 데 사용
다항 정리	다항 정리를 일반화함
참고
관련 항목	이항 정리 조합론 확률론 블레즈 파스칼

2. 역사

파스칼의 삼각형은 블레즈 파스칼의 이름이 붙었지만, 그 이전부터 여러 문화권에서 발견되었다.

양휘의 삼각형은 주판 숫자를 사용하여 중국에서 묘사되었으며, 주세걸이 1303년에 저술한 수학 저서인 사원옥감에 나타난다.

페르시아의 수학자 알카라지(953–1029)는 현재는 유실된 책을 저술했는데, 이 책에는 파스칼의 삼각형에 대한 최초의 설명이 담겨 있었다.^[4]^[5]^[6] 인도에서는 핑갈라 (기원전 3세기 또는 2세기)가 쓴 ''찬다샤스트라''에 두 종류의 음절을 배열하여 다양한 길이의 운율을 형성하고 그 수를 세는 방법이 암호적으로 설명되어 있다. 핑갈라의 10세기 해설자 할라유다가 해석하고 상세히 설명한 바에 따르면, 운율을 세는 그의 "피라미드 전개 방법"(''메루-프라스타라'')은 파스칼의 삼각형과 동일하다. 이 방법은 오마르 하이얌 (1048–1131)에 의해 반복되었으며, 이란에서 '''하이얌의 삼각형''' (مثلث خیام|label=none^fa)이라고도 불린다.^[8] 하이얌은 이항 정리를 포함한 몇 가지 정리를 알고 있었다.^[9]

중국에서는 11세기에 수학자 가헌 (1010–1070)의 저서를 통해 알려졌다. 13세기에는 양휘 (1238–1298)가 이 삼각형을 정의했으며, 중국에서는 '''양휘의 삼각형''' (s=杨辉三角|t=楊輝三角|labels=no^중국어)이라고 불린다.^[10]

유럽에서는 요르다누스 데 네모레의 ''산술'' (13세기)에 처음 등장했다.^[11] 게르소니데스는 14세기 초에 곱셈 공식을 사용하여 이항 계수를 계산했다.^[12] 페트루스 아피아누스 (1495–1552)는 1527년에 출판된 그의 상업 계산 서적 책 표지에 완전한 삼각형을 게재했다.^[13] 미하엘 슈티펠은 1544년에 삼각형의 일부(각 행의 두 번째 열부터 중간 열까지)를 형상수의 표로 묘사하여 출판했다.^[12] 이탈리아에서는 타르탈리아 (1500–1577)의 이름을 따서 '''타르탈리아의 삼각형'''이라고 부르는데, 타르탈리아는 1556년에 삼각형의 6개 행을 출판했다.^[12] 제로라모 카르다노도 1570년에 삼각형과 이를 구성하는 덧셈 및 곱셈 규칙을 출판했다.^[12]

블레즈 파스칼은 1665년에 사후 출판된 《Traité du triangle arithmétique|산술 삼각형 논고^프랑스어》에서 삼각형에 대해 당시 알려진 몇 가지 결과를 모아 확률론 문제를 푸는 데 사용했다. 이 삼각형은 나중에 피에르 레이몽 드 몽모르 (1708)가 table de M. Pascal pour les combinaisons|파스칼 씨의 조합표^프랑스어라고 부르고 아브라함 드 무아브르 (1730)가 Triangulum Arithmeticum PASCALIANUM|파스칼의 산술 삼각형^la이라고 부르면서 파스칼의 이름이 붙여졌으며, 이것이 현대 서양 명칭의 기반이 되었다.^[15]

한국에서는 조선시대 수학자 홍정하가 그의 저서 《구일집》에서 파스칼의 삼각형과 유사한 내용을 다루었다.

2. 1. 동양

양휘는 의 《석쇄산서》에 있는 '파스칼의 삼각형'을 인용했다.]]

고대 인도의 수학자 Pingala|핑갈라^영어의 저작에 대해 10세기에 Halayudha|할라유다^영어가 쓴 주석인 《무리타산지바니》는 파스칼의 삼각형에 대해 확인할 수 있는 가장 오래된 문헌이다. 핑갈라의 원문은 단편적으로만 현존하지만, 할라유다는 핑갈라의 ''Meru-prastaara''인 '수미산의 계단'이라는 단어를 파스칼의 삼각형을 뜻하는 것으로 해석했다. 할라유다는 삼각형과 피보나치 수와의 관계에 대해서도 이해하고 있었다.^[7]

중국에서는 11세기에 수학자인 Jia Xian|가헌^영어, 13세기에 수학자인 양휘가 이 삼각형을 연구했으며, 중국 내에서는 이 삼각형을 '가헌 삼각형' 또는 '양휘의 삼각형'이라고 부른다.^[10]

페르시아에서는 Al-Karaji|알카라지^영어와 오마르 하이얌이 연구했으며, 이란에서는 '하이얌의 삼각형'이라고 부른다. 하이얌은 이항 정리를 포함한 여러 정리들이 이 삼각형에 포함된다는 것을 알고 있었고, ''n''차 이항 전개의 계수를 구하는 방법을 알고 있었을 것으로 추정된다.^[8]^[9]

2. 2. 서양

유럽에서는 파스칼의 삼각형이 요르다누스 데 네모레의 ''산술'' (13세기)에 처음 등장했다.^[11] 14세기 초에 게르소니데스는 곱셈 공식을 사용하여 이항 계수를 계산했다.^[12] 페트루스 아피아누스 (1495–1552)는 1527년에 출판된 그의 상업 계산 서적 책 표지에 완전한 삼각형을 게재했다.^[13] 미하엘 슈티펠은 1544년에 삼각형의 일부(각 행의 두 번째 열부터 중간 열까지)를 형상수의 표로 묘사하여 출판했다.^[12] 이탈리아에서는 타르탈리아 (1500–1577)의 이름을 따서 '''타르탈리아의 삼각형'''이라고 부르는데, 타르탈리아는 1556년에 삼각형의 6개 행을 출판했다.^[12] 제로라모 카르다노도 1570년에 삼각형과 이를 구성하는 덧셈 및 곱셈 규칙을 출판했다.^[12]

블레즈 파스칼은 1665년에 사후 출판된 《Traité du triangle arithmétique|산술 삼각형 논고^프랑스어》에서 삼각형에 대해 당시 알려진 몇 가지 결과를 모아 확률론 문제를 푸는 데 사용했다. 이 삼각형은 나중에 피에르 레이몽 드 몽모르 (1708)가 table de M. Pascal pour les combinaisons|파스칼 씨의 조합표^프랑스어라고 부르고 아브라함 드 무아브르 (1730)가 Triangulum Arithmeticum PASCALIANUM^la (라틴어: 파스칼의 산술 삼각형)이라고 부르면서 파스칼의 이름이 붙여졌으며, 이것이 현대 서양 명칭의 기반이 되었다.^[15]

3. 구성 및 성질

파스칼의 삼각형은 각 행의 양 끝에 1을 놓고, 그 사이의 숫자들은 윗줄의 인접한 두 숫자의 합으로 채워진다. 예를 들어 3번째 행은 1, 2, 1인데, 여기서 2는 윗줄의 1과 1을 더한 값이다.

파스칼의 삼각형의 n번째 행에서 k번째 항목은

\tbinom nk

로 표시하며, "n choose k"라고 읽는다. 이 표기법을 사용하면 파스칼의 삼각형은 다음과 같은 점화식으로 표현될 수 있다.

:

{n \choose k} = {n-1 \choose k-1} + {n-1 \choose k}

이는 모든 양의 정수

n

과 모든 정수

0 \le k \le n

에 적용된다.^[3] 이 점화식은 파스칼의 법칙으로 알려져 있다.

파스칼의 삼각형에서 ''m''번째 행의 각 숫자의 합은 2^''m''-1이다. 예를 들어 5번째 행의 숫자의 합은 1 + 4 + 6 + 4 + 1 = 16이며, 이 값은 2^5-1과 같다. 이는 2^''m''-1 = (1 + 1)^''m''-1을 이항 전개하면 쉽게 알 수 있다. 1번째 행부터 ''m''번째 행까지의 숫자의 총합은 2^''m'' - 1이 된다.

''m''번째 행에 있는 각 숫자를 제곱해서 더하면 2''m'' - 1 번째 행의 중앙의 수가 된다. 예를 들어 5번째 행에서는 1² + 4² + 6² + 4² + 1² = 70이 되어 9번째 행의 중앙의 수와 일치한다.

어떤 단의 양 끝에서 2번째 수 ''p''가 소수일 때, 그 단의 양 끝을 제외한 숫자는 ''p''의 배수가 된다. 파스칼의 삼각형을 만들고, 각 수의 배수에 색을 칠하면 특정한 모양이 된다.^[41]

삼각형의 각 숫자가 최상단의 위치를 꼭짓점으로 한 비스듬한 격자 위에 있다고 가정했을 때, 각 숫자는 최상단의 1에서 격자의 선을 통과해 최단 거리로 그 장소에 도착하는 경로의 수가 된다.

3. 1. 기본 성질

파스칼의 삼각형에서 각 행의 숫자는 이항 계수를 나타낸다. 즉, n번째 행의 k번째 숫자는

\tbinom nk

(n choose k)와 같다.^[3] n번째 행의 각 숫자들의 합은

2^n

이 된다. 예를 들어 0행의 합은 1, 1행의 합은 2, 2행의 합은 4이다. 홀수 번째 행의 중앙에서 양쪽 두 번째 숫자를 빼면 카탈랑 수가 된다. 예를 들어, 4행의 중앙 숫자인 6에서 양쪽 두 번째 숫자인 1을 빼면 5가 되는데, 이는 세 번째 카탈랑 수이다.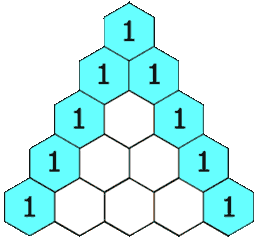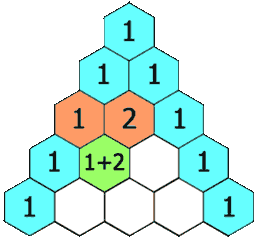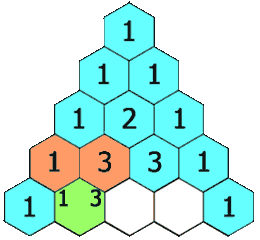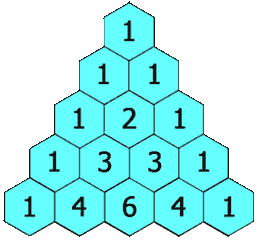

각 행의 원소의 곱은 e와 관련이 있다.^[17]^[18]
$\pi$ 는 닐라칸타 무한 급수를 사용하여 파스칼의 삼각형에서 찾을 수 있다.^[19]
파스칼의 삼각형에 있는 일부 숫자들은 로자니치의 삼각형에 있는 숫자들과 상관관계가 있다.
$n$ 행의 원소의 제곱의 합은 $2n$ 행의 가운데 원소와 같다.^[40] 예를 들어, 1² + 4² + 6² + 4² + 1² = 70이며, 이는 8번째 행의 가운데 숫자와 같다.
$p$ 행에서 $p$ 가 소수이면, 그 행의 모든 항은 1을 제외하고는 $p$ 로 나누어 떨어진다.
$n$ 행에서 홀수 항의 수를 세려면, $n$ 을 이진법으로 변환한다. 이진 표현에서 1의 개수를 $x$ 라고 하면, 홀수 항의 수는 $2^x$ 가 된다. 이 숫자들은 굴드의 수열의 값이다.^[20]
2^''n'' − 1행 (''n'' ≥ 0)의 모든 항목은 홀수이다.^[21]
파스칼의 삼각형 행의 원소를 번갈아 더하고 빼면 결과는 0이 된다. 예를 들어, 6행은 1, 6, 15, 20, 15, 6, 1이므로, 1 − 6 + 15 − 20 + 15 − 6 + 1 = 0이다.

파스칼의 삼각형은 이항 전개에 자주 사용된다. 예를 들어, (x+y)² = x² + 2xy + y²의 각 계수는 삼각형의 3번째 행의 수 1, 2, 1과 일치한다.

이항 계수는 조합의 수이기도 하므로, 조합론에서도 파스칼의 삼각형은 유용하다.

파스칼의 삼각형의 가장 단순한 성질은 다음과 같다.

꼭대기에서 양쪽 아래 방향으로 나열된 숫자는 모두 1이다.
2행의 1에서 양쪽 아래 방향에는 자연수가 나타난다.
3행의 1에서 양쪽 아래 방향에는 삼각수가 나타난다.
4행의 1에서 양쪽 아래 방향에는 삼각뿔수가 나타난다.
5행의 1에서 양쪽 아래 방향에는 오포체수가 나타난다.
일반적으로 ''n'' 행의 1에서 양쪽 아래 방향에는 ''n'' − 1 차원 단순체 수가 나타난다.

thumb

다른 성질로는 피보나치 수에 관한 것이 있다. 왼쪽 두번째 열의 임의의 숫자에서 나이트가 뛰어넘는 것처럼 비스듬히 숫자를 골라 그 합계를 취하면 피보나치 수가 된다.

3. 2. 수열과의 관계

파스칼의 삼각형의 대각선에는 다양한 수열이 나타난다. 가장 바깥쪽 대각선에는 모두 1이, 그 다음 대각선에는 자연수가, 그 다음에는 삼각수, 사각뿔수(삼각뿔수), 오포체수 등의 수열이 순서대로 나타난다.^[41] 일반적으로 ''n''번째 대각선에는 ''n'' - 1 차원 단순체 수가 나타난다.

파스칼의 삼각형에서 얕은 대각선의 합은 피보나치 수열을 이룬다. 예를 들어, 왼쪽 두 번째 열의 임의의 숫자에서 시작하여 나이트가 이동하는 것처럼 대각선으로 숫자를 선택하여 더하면 피보나치 수를 얻을 수 있다. 5번째 행의 4에서 시작하여 4, 10, 6, 1을 선택하면 그 합은 21이 된다.^[41]

짝수 번째 행에서 중앙 숫자를 기준으로 왼쪽 두 번째 숫자를 빼면 카탈랑 수를 얻을 수 있다. 예를 들어, 7번째 행의 중앙 숫자 20에서 양옆의 6을 빼면 14가 되는데, 이는 4번째 카탈랑 수이다.^[41]

4. 이항 전개

파스칼의 삼각형은 이항정리에서 계수들의 값을 계산하는 데 사용된다. 예를 들어,

:(x + 1)^2 = 1 \cdot x^2 + 2 \cdot x + 1

이라는 식에서 각 계수인 1, 2, 1은 파스칼의 삼각형의 3번째 줄에 해당한다.

일반적으로,

:(x + y)^n = a_0 x^n y^0 + a_1 x^{n-1} y^1 + a_2 x^{n-2} y^2 + \cdots +a_{n-2}x^{2} y^{n-2}+a_{n-1} x^1 y^{n-1}+ a_{n} x^0 y^n

과 같은 전개식에서, a_i는 파스칼의 삼각형의 (n+1)번째 행의 (k)번째 열의 값과 순차적으로 대응된다.

이항 전개에서 발생하는 계수는 파스칼의 삼각형으로 결정된다. 예를 들어,

:(x + y)^2 = x^2 + 2xy + y^2 = \mathbf{1} x^2 y^0 + \mathbf{2} x^1 y^1 + \mathbf{1} x^0 y^2,

전개에서 계수는 파스칼의 삼각형의 두 번째 행의 항목이다.

일반적으로 이항 정리는 (x + y)와 같은 이항식이 양의 정수 거듭제곱 n으로 거듭제곱될 때, 식은 다음과 같이 전개된다고 말한다.

:(x + y)^n = \sum_{k=0}^{n} a_{k} x^{n-k} y^{k} = a_{0} x^n + a_{1} x^{n - 1} y + a_{2} x^{n - 2} y^{2} + \ldots + a_{n - 1} x y^{n-1} + a_{n} y^{n},

여기서 계수 a_k는 파스칼의 삼각형의 n번째 행의 숫자와 정확히 같다.

:a_k = {n \choose k}.

파스칼의 삼각형의 맨 왼쪽 대각선 전체는 이항 전개에서 x^n의 계수에 해당하고, 다음 왼쪽 대각선은 x^{n-1} y의 계수에 해당한다.

이항 정리가 파스칼의 삼각형의 구성과 어떻게 관련되는지 보려면 (x + y)^{n + 1}의 전개의 계수를 (x + 1)^{n}의 해당 계수로 계산하는 문제를 고려한다. 여기서 편의를 위해 y = 1로 설정한다.

:(x + 1)^{n} = \sum_{k = 0}^{n} a_{k} x^{k}.

:(x+1)^{n+1} = (x+1)(x+1)^n = x(x+1)^n + (x+1)^n = \sum_{i=0}^n a_i x^{i+1} + \sum_{k=0}^n a_k x^k.

두 합은 k=i+1로 재색인화될 수 있으며 결합하여 다음을 생성한다.

:\begin{align}

\sum_{i=0}^{n} a_{i} x^{i+1} + \sum_{k=0}^n a_k x^k &=

\sum_{k=1}^{n+1} a_{k-1} x^{k} + \sum_{k=0}^n a_k x^k \\ [4pt] &=

\sum_{k=1}^{n} a_{k-1} x^{k} + a_{n}x^{n+1} + a_0x^0 + \sum_{k=1}^n a_k x^k \\[4pt] &=

a_0x^0 + \sum_{k=1}^{n} (a_{k-1} + a_k)x^{k} + a_{n}x^{n+1} \\[4pt] &=

x^0 + \sum_{k=1}^{n} (a_{k-1} + a_k)x^{k} + x^{n+1}.

\end{align}

따라서 맨 왼쪽 및 맨 오른쪽 계수는 1로 유지되며, 주어진 0 < k < n + 1에 대해 다항식 (x + 1)^{n + 1}에서 x^{k} 항의 계수는 이전 거듭제곱 (x + 1)^n에서 x^{k-1} 및 x^{k} 계수의 합인 a_{k-1} + a_{k}와 같다. 이것은 파스칼의 삼각형을 구성하기 위한 규칙이다.

(a + b)^{n} = b^{n}(\tfrac{a}{b} + 1 )^{n}이므로 일반적인 경우의 전개에서 계수는 동일하다.

이항 정리의 흥미로운 결과는 두 변수 모두 x = y = 1로 설정하여 얻는다.

: \sum_{k = 0}^{n} {n \choose k} = {n \choose 0} + {n \choose 1} + \cdots + {n \choose n-1} + {n \choose n} = (1+1)^n = 2^{n}.

즉, 파스칼의 삼각형의 n번째 행에 있는 항목의 합은 2의 n제곱이다.

:(x+y)^2=x^2+2xy+y^2

의 각 계수는 삼각형의 3번째 행의 수 1, 2, 1과 일치한다. 일반적으로

:(x+y)^n=a_0x^n+a_1x^{n-1}y+a_2x^{n-2}y^2+\cdots+a_{n-1}xy^{n-1}+a_ny^n

라고 하면, a_i 들은 파스칼의 삼각형의 n + 1 번째 행에 있는 숫자이다. 이것은 수학적 귀납법으로 증명할 수 있다. 먼저, n = 0인 경우는 명백하다. 다음으로,

:(x+y)^n=\sum_{i=0}^n a_i x^{n-i}y^i

라고 하면,

:\begin{align}

(x+y)^{n+1}

&=x(x+y)^n+y(x+y)^n \\

&=\sum_{i=0}^n a_i x^{n-i+1} y^i+\sum_{i=0}^n a_i x^{n-i} y^{i+1} \\

&=\sum_{i=0}^n a_i x^{n-i+1} y^i+\sum_{i=1}^{n+1} a_{i-1} x^{n-i+1} y^i \\

&=a_0x^{n+1}+\sum_{i=1}^n a_i x^{n-i+1} y^i+\sum_{i=1}^n a_{i-1} x^{n-i+1} y^i+a_n y^{n+1} \\

&=x^{n+1}+\sum_{i=1}^n (a_{i-1}+a_i) x^{n-i+1} y^i+y^{n+1}

\end{align}

이 된다.

5. 조합

조합 계산에 파스칼의 삼각형을 활용할 수 있다. $n$ 개의 항목 중 $k$ 개를 선택하는 조합의 수, 즉 $n$ 개의 원소 중에서 $k$ 개의 원소를 갖는 부분 집합의 수는 다음 식으로 구할 수 있다.

: $\mathbf{C}(n, k) = \mathbf{C}_{k}^{n}= = {n \choose k} = \frac{n!}{k!(n-k)!}$ .

이 값은 파스칼의 삼각형에서 $n$ 번째 행의 $k$ 번째 항목과 같다. 곱셈 계산을 하는 대신, 삼각형(덧셈으로 구성)에서 해당 항목을 찾으면 된다. 예를 들어, 7명의 후보자 중에서 3명의 직원을 고용해야 한다면, 가능한 고용 선택의 수는 7 콤비네이션 3, 즉 위 표의 7번째 행의 3번째 항목인 $\tbinom{7}{3}=35$ 이다.^[16]

행 또는 대각선의 모든 요소를 다른 요소나 팩토리얼을 계산하지 않고 계산하는 간단한 알고리즘이 존재한다.

요소 $\tbinom{n}{0}, \tbinom{n}{1}, \ldots, \tbinom{n}{n}$ 을 갖는 행 $n$ 을 계산하려면 $\tbinom{n}{0}=1$ 로 시작한다. 각 후속 요소에 대해 값은 이전 값에 분자를 약간 변경하고 분모를 변경하는 분수를 곱하여 결정된다.

: ${n\choose k}= {n\choose k-1}\times \frac{n+1-k}{k}.$

예를 들어, 행 5를 계산하려면 분수는 $\tfrac{5}{1}$ , $\tfrac{4}{2}$ , $\tfrac{3}{3}$ , $\tfrac{2}{4}$ 및 $\tfrac{1}{5}$ 이며, 따라서 요소는 $\tbinom{5}{0}=1$ , $\tbinom{5}{1}=1\times\tfrac{5}{1}=5$ , $\tbinom{5}{2}=5\times\tfrac{4}{2}=10$ 등이다. (나머지 요소는 대칭에 의해 쉽게 구할 수 있다.)

요소 $\tbinom{n}{0}, \tbinom{n+1}{1}, \tbinom{n+2}{2},\ldots,$ 를 포함하는 대각선을 계산하려면 다시 $\tbinom{n}{0} = 1$ 로 시작하고 특정 분수를 곱하여 후속 요소를 얻는다.

: ${n+k\choose k}= {n+k-1\choose k-1}\times \frac{n+k}{k}.$

예를 들어, $\tbinom{5}{0}$ 에서 시작하는 대각선을 계산하려면 분수는 $\tfrac{6}{1}, \tfrac{7}{2}, \tfrac{8}{3}, \ldots$ 이고, 요소는 $\tbinom{5}{0}=1, \tbinom{6}{1}=1 \times \tfrac{6}{1}=6, \tbinom{7}{2}=6\times\tfrac{7}{2}=21$ 등이다. 대칭에 의해, 이러한 요소는 $\tbinom{5}{5}, \tbinom{6}{5}, \tbinom{7}{5}$ 등과 같다.

이항 계수는 조합의 수이기도 하므로, 조합론에서도 파스칼의 삼각형은 유용하다. ''n''개의 것에서 서로 다른 ''k''개를 선택하는 방법 _''n''''C''_''k''의 값은 파스칼의 삼각형의 (''n'' + 1)번째 행의 처음부터 (''k'' + 1)번째 수와 같다.

6. 확률 분포

파스칼의 삼각형의 $n$ 번째 행을 $2^n$ 으로 나누면 $p = \tfrac{1}{2}$ 인 대칭적인 경우의 이항 분포가 된다. 중심 극한 정리에 따르면, 이 분포는 $n$ 이 증가함에 따라 정규 분포에 접근한다. 이는 조합 공식에 포함된 팩토리얼에 스털링 근사를 적용하여 볼 수도 있다.

이는 두 가지 방식으로 이산 컨볼루션 연산과 관련이 있다. 첫째, 다항식 곱셈은 정확히 이산 컨볼루션에 해당하므로, 수열 $\{ \ldots, 0, 0, 1, 1, 0, 0, \ldots \}$ 을 반복적으로 자신과 컨볼루션하는 것은 $x + 1$ 의 거듭제곱을 취하는 것과 같으며, 따라서 삼각형의 행을 생성하는 것과 같다. 둘째, 확률 변수에 대한 분포 함수를 반복적으로 자신과 컨볼루션하는 것은 해당 변수의 독립적인 ''n''개의 복사본의 합에 대한 분포 함수를 계산하는 것과 같다. 이것은 정확히 중심 극한 정리가 적용되는 상황이며, 따라서 극한에서 정규 분포를 얻는다. (어떤 것을 반복적으로 자신과 컨볼루션하는 연산을 컨볼루션 멱이라고 한다.)

7. 패턴

파스칼의 삼각형은 여러 가지 숫자 패턴을 포함하고 있다.

각 프레임은 파스칼의 삼각형의 한 행을 나타낸다. 픽셀의 각 열은 이진법으로 표현된 숫자이며 최하위 비트가 아래에 있다. 밝은 픽셀은 1을, 어두운 픽셀은 0을 나타낸다.

''n'' + 1을 ''k'' + 1 개의 정렬된 파티션으로 분할하는 조합의 수는 파스칼의 삼각형을 형성한다.

파스칼의 삼각형의 행을 왼쪽으로 정렬하면, 아래 색상으로 구분된 대각선 띠들의 합은 피보나치 수가 된다.

1
1	1
1	2	1
1	3	3	1
1	4	6	4	1
1	5	10	10	5	1
1	6	15	20	15	6	1
1	7	21	35	35	21	7	1

''n''개에서 서로 다른 ''k''개를 선택하는 방법의 수 _''n''''C''_''k''는 파스칼의 삼각형에서 (''n'' + 1)번째 행의 처음부터 (''k'' + 1)번째 수와 같다. 1 ≤ ''k'' ≤ ''n'' − 1일 때, 이는 ''n'' − 1 차원 단체의 ''k'' − 1 차원 면의 수이기도 하다. 예를 들어, 5번째 행의 처음부터 2번째 수인 4는 사면체(3차원 단체)의 꼭짓점(0차원 면)의 수이고, 3번째 수인 6은 모서리(1차원 면)의 수이며, 4번째 수인 4는 면(2차원 면)의 수이다. 이는 사면체의 경우, 두 개의 꼭짓점을 잇는 선분의 집합은 모서리의 집합과 같고, 세 개의 꼭짓점을 잇는 삼각형의 집합은 면의 집합과 같기 때문이다.^[40] 양쪽 끝의 1은 공집합(-1차원 면)과 전체 집합(3차원 면)의 수로 해석할 수 있다.

7. 1. 시에르핀스키 삼각형

파스칼의 삼각형의 처음 32개 행에서 이항 계수가 짝수이면 흰색, 홀수이면 검은색으로 음영 처리하여 얻은 4단계 시에르핀스키 삼각형 근사치

파스칼의 삼각형에서 홀수를 색칠하면 프랙탈인 시에르핀스키 삼각형과 매우 유사한 패턴이 나타난다. 이 유사성은 더 많은 행을 고려할수록 더욱 정확해진다. 행의 수가 무한대에 접근하는 극한에서, 결과 패턴은 고정된 둘레를 가질 때 실제로 시에르핀스키 삼각형이 된다.^[22]

일반적으로, 숫자를 3, 4 등의 배수인지 여부에 따라 다르게 색칠하면 다른 유사한 패턴을 얻을 수 있다. 검은색 숫자의 비율이 ''n''이 증가함에 따라 0에 가까워지므로, 홀수 이항 계수의 비율도 ''n''이 무한대에 접근함에 따라 0에 가까워진다.^[22]

7. 2. 경로의 수

격자에서 특정 지점까지 이동하는 최단 경로의 수는 파스칼의 삼각형의 숫자로 주어진다.

8. 일반화

파스칼의 삼각형은 더 높은 차원으로 일반화할 수 있다. 3차원 형태는 파스칼의 피라미드 또는 파스칼의 4면체라고 불리며, 더 높은 차원의 유사체는 일반적으로 "파스칼의 단체"라고 불린다.^[40]

파스칼의 삼각형의 3번째 줄(1, 3, 3, 1)을 예로 들어보면, 2차원 삼각형은 하나의 2차원 요소(자기 자신), 세 개의 1차원 요소(선 또는 변), 세 개의 0차원 요소(꼭짓점)를 갖는다. 사면체는 하나의 3차원 요소(자기 자신), 네 개의 2차원 요소(면), 여섯 개의 1차원 요소(변), 네 개의 0차원 요소(꼭짓점)를 가지는데, 여기에 마지막 1을 더하면 삼각형의 4번째 행(1, 4, 6, 4, 1)과 일치한다. 이러한 패턴은 단순체라고 불리는 더 높은 차원의 도형으로 확장된다.

이 패턴은 (''n'' − 1)-단순체에서 ''n''-단순체를 만들 때, 기존 단순체 바깥에 새로운 꼭짓점을 추가하고 이를 기존의 모든 꼭짓점과 연결하는 방식으로 이해할 수 있다. 사면체의 경우, 원래 삼각형의 요소 수에 새로운 꼭짓점으로부터 생성되는 요소 수를 더하면 파스칼의 삼각형에서 다음 행의 숫자를 얻는 것과 같은 원리가 적용된다.

(''x'' + 1)^''n''의 계수는 파스칼의 삼각형의 n번째 행을 나타낸다. (''x'' − 1)^''n''의 계수는 동일하지만 부호가 +1과 −1로 번갈아 나타난다. sin(''x'')^''n''+1/''x''의 푸리에 변환에서도 이와 유사한 숫자 패턴이 나타난다.^[25]

8. 1. 고차원 확장

파스칼의 삼각형은 더 높은 차원으로 확장할 수 있다. 3차원 형태는 파스칼의 피라미드 또는 파스칼의 사면체라고 불린다. 더 높은 차원의 유사체는 일반적으로 "파스칼의 단체"라고 통칭한다.^[40]

삼각형이 아닌 정사각형과 관련된 패턴을 살펴보면,

(x + 2)

의 계수를 사용하는 파스칼의 삼각형과 유사한 형태를 구성할 수 있다. 이는

(x + 1)

을 사용하는 일반적인 파스칼의 삼각형과는 다르다. 이 유사 삼각형을 만드는 방법 중 하나는 다음과 같은 규칙을 따르는 것이다.

:

{n \choose k} = 2\times{n-1 \choose k-1} + {n-1 \choose k}.

즉, 파스칼의 삼각형처럼 숫자 쌍을 선택하지만, 더하기 전에 왼쪽 숫자를 두 배로 만든다. 이렇게 만들어진 삼각형은 다음과 같다.

:

\begin{matrix}\text{  1} \\\text{  1}   \quad \text{  2} \\\text{  1}   \quad \text{  4}   \quad \text{  4} \\\text{  1}   \quad\text{  6}   \quad   \text{ 12}   \quad\text{  8} \\\text{  1}   \quad\text{  8}   \quad   \text{ 24}   \quad  \text{ 32}   \quad  \text{ 16} \\\text{  1}   \quad   \text{ 10}   \quad  \text{ 40}   \quad  \text{ 80}   \quad  \text{ 80}    \quad  \text{ 32} \\\text{  1}   \quad  \text{ 12}   \quad  \text{ 60}   \quad  160   \quad 240  \quad  192   \quad   \text{ 64} \\\text{  1}   \quad  \text{ 14}   \quad  \text{ 84}   \quad  280  \quad  560  \quad  672   \quad  448   \quad   128\end{matrix}

이 삼각형을 구성하는 또 다른 방법은 파스칼의 삼각형에서 시작하여 각 항목에 2^k를 곱하는 것이다. 여기서 k는 해당 숫자의 행에서의 위치이다. 예를 들어, 파스칼의 삼각형의 4번째 행에서 2번째 값은 6이다. 유사 삼각형에서 해당 위치의 값을 얻으려면 6에

2^2=4

를 곱한다.

이렇게 구성된 유사 삼각형을 통해 임의의 차원을 가진 정육면체(초정육면체)를 구성하는 요소의 수를 파악할 수 있다. 예를 들어, 2차원 정육면체(정사각형)는 1개의 2차원 요소, 4개의 1차원 요소(변), 4개의 0차원 요소(점)를 가지며, 이는 표의 2번째 행 (1, 4, 4)와 일치한다. 정육면체는 1개의 정육면체, 6개의 면, 12개의 모서리, 8개의 정점을 가지며, 이는 유사 삼각형의 다음 행 (1, 6, 12, 8)에 해당한다. 이 패턴은 무한히 계속된다.

이 삼각형에서 행 ''m''에 있는 요소의 합은 3^''m''과 같다. 예를 들어, 4번째 행의 요소 합은 1 + 8 + 24 + 32 + 16 = 81이며, 이는

3^4 = 81

과 같다.

8. 2. 복소수 확장

파스칼의 삼각형의 3번째 줄(1, 3, 3, 1)은 2차원 삼각형을 나타내는데, 이는 하나의 2차원 요소(자신), 세 개의 1차원 요소(선 또는 변), 세 개의 0차원 요소(꼭짓점)를 갖는다. 마지막 숫자 1은 아래에서 설명한다. 사면체는 하나의 3차원 요소(자신), 네 개의 2차원 요소(면), 여섯 개의 1차원 요소(변), 네 개의 0차원 요소(꼭짓점)를 가지며, 마지막 1을 더하면 삼각형의 4번째 행(1, 4, 6, 4, 1)과 일치한다. 1행은 점, 2행은 선분(쌍)에 해당하며, 이 패턴은 단순체라고 불리는 더 높은 차원의 초사면체로 이어진다.

이 패턴은 (''n'' − 1)-단순체에서 ''n''-단순체를 만드는 과정이 기존 단순체 바깥에 새로운 꼭짓점을 추가하고, 이를 기존 꼭짓점과 연결하는 방식으로 이해할 수 있다. 예를 들어 삼각형에서 사면체를 만들 때, 삼각형의 요소는 파스칼의 삼각형 3번째 행으로 나타낼 수 있다( '''1''' 면, '''3''' 변, '''3''' 꼭짓점). 새로운 꼭짓점을 삼각형 평면 위에 놓고, 원래 삼각형의 세 꼭짓점과 연결한다.

사면체에서 주어진 차원의 요소 수는 두 숫자의 합으로 나타낼 수 있다. 첫째는 원래 삼각형에 있던 해당 요소의 수이고, 둘째는 "각각 원래 삼각형의 한 차원 적은 요소 위에 구축된" 새로운 요소의 수이다. 따라서 사면체에서 세포 (다면체 요소)의 수는 1이다. 면의 수는 4이다. 변의 수는 6이다. 새로운 꼭짓점의 수는 4이다. 이처럼 주어진 차원의 요소 수를 한 차원 적은 요소의 수에 더하여 다음 상위 단순체에서 발견되는 요소 수를 구하는 과정은 파스칼의 삼각형에서 한 행의 두 인접한 숫자를 더하여 아래 숫자를 얻는 과정과 같다. 파스칼의 삼각형 행에서 마지막 숫자(1)는 해당 행으로 표시된 단순체에 추가되어 다음 상위 단순체를 생성할 새로운 꼭짓점을 의미한다. 이 꼭짓점은 원래 단순체의 모든 요소에 연결되어 새로운 단순체에서 한 차원 더 높은 새로운 요소를 생성하며, 이는 파스칼의 삼각형에서 보이는 패턴과 같다.

파스칼의 삼각형 각 행은 ''n''차원 초정육면체에서 고정된 꼭짓점으로부터 각 거리에 있는 꼭짓점의 수를 나타낸다. 예를 들어 3차원에서 3번째 행(1 3 3 1)은 일반적인 3차원 정육면체에 해당한다. 꼭짓점 ''V''를 고정하면, ''V''로부터 거리가 0인 꼭짓점(즉, ''V'' 자체)이 하나, 거리가 1인 꼭짓점이 세 개, 거리가 ²인 꼭짓점이 세 개, 거리가 ³인 꼭짓점(''V''의 반대편 꼭짓점)이 하나 있다. 2번째 행은 정사각형, 더 큰 행은 각 차원의 초정육면체에 해당한다.

8. 3. 임의의 밑(Base) 확장

파스칼의 삼각형의 3번째 줄(1, 3, 3, 1)을 생각해보자. 2차원 삼각형은 하나의 2차원 요소(자신), 세 개의 1차원 요소(선 또는 변), 세 개의 0차원 요소(꼭짓점)를 갖는다. 예를 들어, 사면체는 하나의 3차원 요소(자신), 네 개의 2차원 요소(면), 여섯 개의 1차원 요소(변), 네 개의 0차원 요소(꼭짓점)를 갖는다. 1을 더하면, 이 값들은 삼각형의 4번째 행(1, 4, 6, 4, 1)에 해당한다. 1행은 점에 해당하고, 2행은 선분(쌍)에 해당한다. 이 패턴은 임의로 높은 차원의 초사면체(단순체)까지 계속된다.

이 패턴은 (''n'' − 1)-단순체로부터 ''n''-단순체를 구성하는 과정이 새로운 꼭짓점을 추가하는 것으로 이루어진다는 것을 이해하면 알 수 있다. 이 새로운 꼭짓점은 기존 단순체의 공간 바깥에 위치하고, 모든 기존 꼭짓점에 연결된다. 예를 들어, 삼각형으로부터 사면체를 구성하는 경우, 삼각형의 요소들은 파스칼의 삼각형의 3번째 행으로 열거된다. 삼각형으로부터 사면체를 구성하려면, 삼각형의 평면 위에 새로운 꼭짓점을 놓고 이 꼭짓점을 원래 삼각형의 세 꼭짓점에 모두 연결한다.

사면체에서 주어진 차원의 요소의 수는 두 숫자의 합이다. 첫째는 원래 삼각형에서 발견된 해당 요소의 수이고, 둘째는 "각각 원래 삼각형의 한 차원 적은 요소 위에 구축된" 새로운 요소의 수이다. 따라서 사면체에서 세포(다면체 요소)의 수는 1+0=1이다. 면의 수는 1+3=4이고, 변의 수는 3+3=6이다. 새로운 꼭짓점의 수는 3+1=4이다. 주어진 차원의 요소의 수를 한 차원 더 적은 요소의 수에 더하여 다음 상위 단순체에서 발견되는 전자의 수를 구하는 이 과정은 파스칼의 삼각형의 한 행에서 두 개의 인접한 숫자를 더하여 아래 숫자를 얻는 과정과 동일하다. 파스칼의 삼각형의 행에서 마지막 숫자(1)는 해당 행으로 표시된 단순체에 추가되어 다음 행으로 표시된 다음 상위 단순체를 생성할 새로운 꼭짓점을 나타낸다. 이 새로운 꼭짓점은 원래 단순체의 모든 요소에 연결되어 새로운 단순체에서 한 차원 더 높은 새로운 요소를 생성하며, 이는 파스칼의 삼각형에서 볼 수 있는 패턴과 동일하다.

(''x'' + 1)^''n''의 계수는 삼각형의 n번째 행이다. (''x'' − 1)^''n''의 계수는 동일하지만 부호가 +1에서 −1로 번갈아 나타난다. 적절한 정규화 후, sin(''x'')^''n''+1/''x''의 푸리에 변환에서도 동일한 숫자 패턴이 나타난다.^[25] 예를 들어, 다음으로부터 발생하는 계단 함수의 값은 다음과 같다.

:Re|실수부^영어(푸리에 [ sin(x)⁵/x ])

번갈아 나타나는 부호로 삼각형의 4번째 행을 구성한다. 이것은 다음 기본 결과의 일반화이다.^[26]

:Re|실수부^영어(푸리에[sin(x)/x])

는 구형파 함수이다. 해당 삼각형의 행은 0행이며, 숫자 1로 구성된다.

만약 n이 4로 나눈 합동 관계에서 2 또는 3과 합동이라면, 부호는 −1로 시작한다. (정규화된) 첫 번째 항의 시퀀스는 i의 거듭제곱에 해당하며, 복소 평면에서 단위 원과 축의 교차점을 순환한다.

9. 응용

파스칼의 삼각형은 컴퓨터 과학 분야에서 활용될 수 있다. 예를 들어, 파이썬, 스칼라, C# 등의 프로그래밍 언어를 사용하여 파스칼의 삼각형을 구현할 수 있다.

9. 1. 컴퓨터 과학

파이썬, 스칼라, C# 등의 프로그래밍 언어를 사용하여 파스칼의 삼각형을 구현할 수 있다.

파이썬 코드 예시:

```python

def pTriangle(n):

p = []

for row in range(n):

tmp = [1] * (row + 1)

for col in range(1, row):

tmp[col] = p[row-1][col-1] + p[row-1][col]

p.append(tmp)

return p

```

스칼라 코드 예시:

```scala

//파스칼 삼각형 소스코드

var height:Int = 0

def pTriangle(given:Array[Int], stop:Int):Unit = {

println(given.deep.toString)

height = height + 1

if (height < stop) {

val next = Array.ofDim[Int](given.length + 1)

for (i <- 0 until next.length) {

if (i == 0 || i == next.length-1) next(i) = 1

else next(i) = given(i-1) + given(i)

}

pTriangle(next, stop)

} else {

height = 0

}

}

```

C# 코드 예시:

```csharp

public class PascalsTriangle

{

static void PascalTriangle(int n)

{

for (int line = 1; line <= n; line++)

{

int c = 1;

for (int i = 1; i <= line; i++)

{

Console.WriteLine(c);

c = c * (line - i) / i;

}

Console.WriteLine("\n");

}

}

public static int Main(int input)

{

PascalTriangle(input);

return input;

}

}

10. 소스 코드

파스칼의 삼각형은 더 높은 차원으로 일반화할 수 있다. 3차원 버전은 '''파스칼의 피라미드''' 또는 '''파스칼의 사면체'''로 알려져 있으며, 일반화된 버전은 '''파스칼의 심플렉스'''로 알려져 있다.

10. 1. 파이썬

python

def pTriangle(n):

p = []

for row in range(n):

tmp = [1] * (row + 1)

for col in range(1, row):

tmp[col] = p[row - 1][col - 1] + p[row - 1][col]

p.append(tmp)

return p

10. 2. 스칼라

scala

// 파스칼 삼각형 소스코드

var height: Int = 0

def pTriangle(given: Array[Int], stop: Int): Unit = {

println(given.deep.toString)

height = height + 1

if (height < stop) {

val next = Array.ofDim[Int](given.length + 1)

for (i <- 0 until next.length) {

if (i == 0 || i == next.length - 1) next(i) = 1

else next(i) = given(i - 1) + given(i)

}

pTriangle(next, stop)

} else {

height = 0

}

}

10. 3. C#

파스칼의 삼각형은 더 높은 차원으로 일반화할 수 있다. 3차원 버전은 ''파스칼의 피라미드'' 또는 ''파스칼의 사면체''로 알려져 있으며, 일반화된 버전은 ''파스칼의 심플렉스''로 알려져 있다.

참조

_[1] 서적 History of Indian Literature
_[2] 서적 Cambridge University Library: the great collections https://books.google[...] Cambridge University Press
_[3] 문서 The binomial coefficient
_[4] 서적 Encyclopaedia of the History of Science, Technology, and Medicine in Non-Western Cultures https://books.google[...] Springer Science & Business Media 2008-03-12
_[5] 서적 The Development of Arabic Mathematics Between Arithmetic and Algebra - R. Rashed https://books.google[...]
_[6] 서적 From Alexandria, Through Baghdad: Surveys and Studies in the Ancient Greek and Medieval Islamic Mathematical Sciences in Honor of J.L. Berggren https://books.google[...] Springer Science & Business Media 2013-10-30
_[7] 간행물 The Pratyayas: Indian Contribution to Combinatorics https://insa.nic.in/[...]
_[8] 서적 Omar Khayyam. The Mathematics Teacher 1958 National Council of Teachers of Mathematics
_[9] 간행물 The story of the binomial theorem
_[10] 서적 CRC concise encyclopedia of mathematics
_[11] 간행물 The arithmetical triangle of Jordanus de Nemore 1989-08-01
_[12] 서적 Combinatorics: Ancient and Modern Oxford University Press
_[13] 서적 Nature of Mathematics https://books.google[...] Cengage Learning
_[14] 웹사이트 Traité du triangle arithmétique, avec quelques autres petits traitez sur la mesme matière https://gallica.bnf.[...]
_[15] 간행물 The Binomial Coefficient Function 1996-01
_[16] 웹사이트 Pascal's Triangle in Probability http://5010.mathed.u[...] 2023-06-01
_[17] 간행물 Finding e in Pascal's triangle
_[18] 간행물 Pascal's triangle: The hidden stor-''e''
_[19] 간행물 Nilakantha's Footprints in Pascal's Triangle
_[20] 간행물 Binomial coefficients modulo a prime
_[21] 간행물 Pascal's triangle and the Tower of Hanoi
_[22] 서적 How to Cut a Cake Oxford University Press
_[23] 웹사이트 The Algebra Of Geometry https://github.com/G[...]
_[24] 서적 Regular Polytopes https://books.google[...] Courier Corporation 1973-01-01
_[25] 간행물 Solvent suppression in Fourier transform nuclear magnetic resonance
_[26] 서적 An Introduction to Digital Signal Processing https://books.google[...] Elsevier
_[27] 서적 Symmetry 2 Pergamon
_[28] 서적 Symmetry 2 Pergamon
_[29] 간행물 A Treatise of the Method of Fluxions and Infinite Series https://www.loc.gov/[...]
_[30] 간행물 Pascal's Triangle and powers of 11
_[31] 간행물 Newton's Unfinished Business: Uncovering the Hidden Powers of Eleven in Pascal's Triangle https://ecommons.uda[...]
_[32] 간행물 Finding any row of Pascal's triangle extending the concept of power of 11 https://www.research[...]
_[33] 간행물 Pascal's Triangle and Powers of 11
_[34] 간행물 A generalization of Pascal's triangle using powers of base numbers https://ambp.centre-[...]
_[35] 서적 Symmetry 2 Pergamon
_[36] 논문 More on Pascal's Triangle and powers of 11
_[37] 논문 Even more on Pascal's Triangle and Powers of 11
_[38] 논문 Extending Pascal's Triangle
_[39] 문서 最上段には実質的な意味はなく、2段目の二つの1を1段目として紹介される場合もある。この方が以下で説明する数式が簡単になる（1を引いたり足したりする必要がなくなる）場合が多い。最上段がないと三角形ではなく台形となるが、この図形は無限に大きく、最下段（底辺）も存在しない。
_[40] 문서 二つの面が共有する線分の集合が辺の集合、三つの面が共有する点の集合が頂点の集合と考えてもよい。また3^''n'' = (1 + 2)^''n'' = (2 + 1)^''n'' を二項展開すればn次元の[[正軸体]]と[[超立方体]]の各次元面の数字が現れる。
_[41] 웹사이트 https://javalab.org/[...]
_[42] 문서 三角形（内部の三角形も同様。重心点は掛けない）の一つの頂点から始めて順に ω （1 の虚[[立方根]]の一つ）を掛けた数を合計する。
_[43] 문서 Maurice Winternitz, ''History of Indian Literature'', Vol. III
_[44] 논문 The story of the binomial theorem
_[45] 서적 Cambridge University Library: the great collections https://books.google[...] Cambridge University Press

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com